只要是做数学思维练习,那么,经典的牛吃草问题是一定会碰到的。
所以,今天给儿子做了这道牛吃草问题。
像这样的问题,关键的知识点是要记住,草并不是静态不变的,在牛吃草的时候,草也在不停地生长。
牢记这一点以后,再利用线段法来解题,就会很方便。
问题是这样的:
假设草地是匀速生长的,如果有27头牛来吃草,6天吃完;23头牛9天吃完;请问如果21头牛,几天能把草吃完?
先画线段图如下:
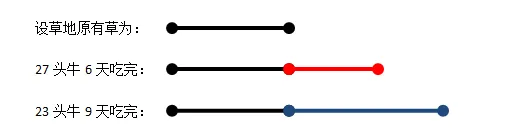
其中,红色线段是6天长的草,蓝色线段是9天长的草。蓝色减去红色就是草地三天长的草。也就是23头牛9天吃完的草,比27头牛6天吃完的多三天长的草。
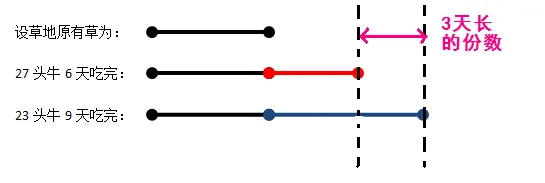
假设一头牛一天吃一份草,则:
27头牛6天吃完,草的份数为:27×6 = 162份
23头牛9天吃完,草的份数为:29×9 = 207份
所以三天长的草是:
207 - 162 = 45份
所以草地每天生长的草是:
45/3 = 15份。
又因为27头牛6天吃完,草的份数为:27×6 = 162份,其中6天长的草量是15×6 = 90份,所以草地原有草为:
162 - 90 = 72份。
现在有21头牛来吃草,如果已知草的总量,除以牛的数量21(因为一头牛一天吃一份草),就能得到天数了。
但是因为草的总量是在不断变化的,没有办法这样求解。接下来就是关键步骤了:
因为草地每天长15份草,那么,我们用15头牛专门吃这长出来的草,就不用再考虑新生长出来的草了。
所以,还剩下21-15 = 6头牛来吃原有的草。这就很简单了:
72/6 = 12天
所以,21头牛来吃草,12天能把草吃完。
类似的牛吃草问题,还有容器同时进水漏水的问题,有场馆人数进进出出的问题等等,都可以用这样的方法来解决。