[STEM之朝思暮想] 6:为他人着想

前言
数学,与我们的生活密不可分,在日常生活中我们常常需要用到加减乘除,买东西需要数学,卖东西需要数学,工作需要数学,发薪日更加需要数学啦,哈哈哈。不过当然也存在着在我们生活中并不需要的数学了,譬如说我接下来要说的,也就是代数(algebra)之一---分式方程(Fractional Equation)。
##分式方程(Fractional Equation)
分式方程,顾名思义也就是由分数方程构成的一串方程式,当我们有一个较为复杂的分数类函数(Function with Numerator and Denominator)需要被简化的时候, 我们会需要部分分式分解(Partial Fraction Decomposition 或 Partial Fraction Expansion)来求解。
这部分分式分解的用途是把一个复杂的函数(分式类,有着分子与分母)分解成两个或多个分数,这些分数的分母为不可约多项式(irreducible polynomial)的分母,而其分子的多项式的次数(power)是不可高于其分母的。在我自己的语言来说,分解出来的分式的分母就是未分解的多项式的根(root),多项式的次数越高,根越多,被分解出来的分式越多。
这解法的概念是由两位伟大的数学家独立发掘的,他们分别是约翰●伯努利(Johann Bernoulli)和哥特弗里德●威廉●莱布尼兹(Gottfried Wilhelm Leibniz)于1702年发现的。这部分分式分解法有许多种方法可以解答,但是我们今天就专注于比较容易让人明白的方式吧,也就是最基本的算法。
例子
虽然我并不适合当老师但我还是姑且当一回吧,以下是一个看起来有一些些复杂的函数:
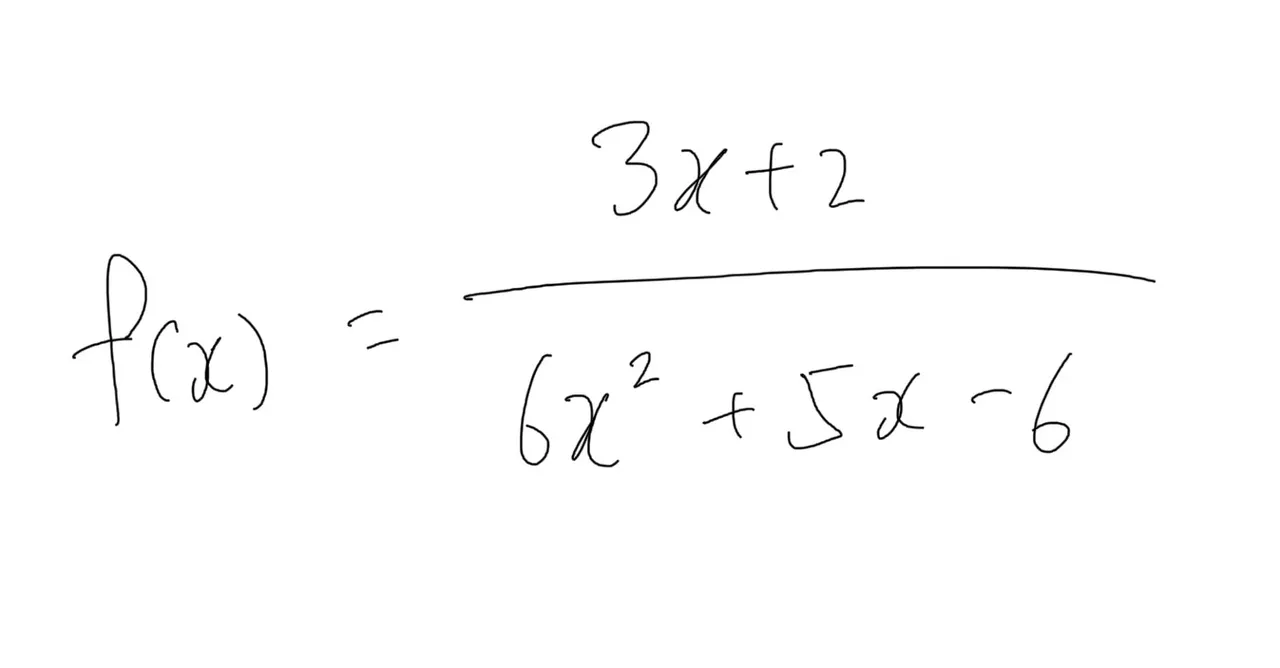
它的分母是可以被分解成两个根的,如下图:
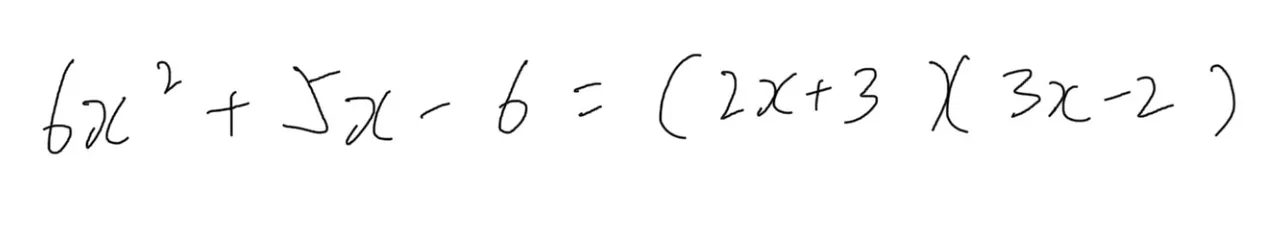
再来,我们把这两个跟变成两个分数各自的分母,并给与各自的分子取名为A和B作为未知数,这就变成如下图中的未知分数方程式啦!
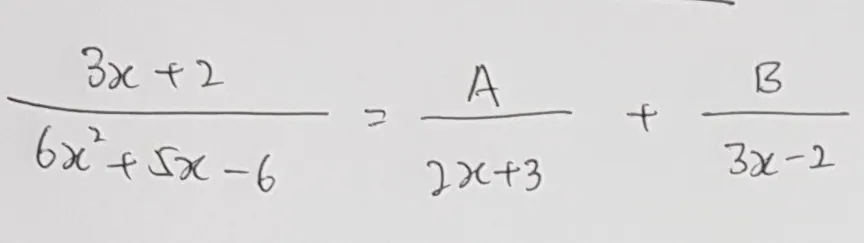
然后,我们必须让两边的分母是一样的,所以我们让A分数(姑且这么叫它吧)的分子分母都乘以B分数的分母。同样的,B分数(姑且这么叫它吧)的分子分母也都乘以A分数的分母(如下图),然后再把等号两边的分母都去掉(因为分母变一样了)。

然后我们得出以下简单一点的方程式了:
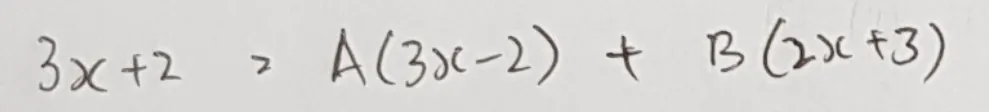
然后我们再移形换位以下,再把左边x的系数和右边x的系数相等,剩下的未知数(没有x的那些)也如出一辙,然后得出以下两个方程式:方程式1和方程式2,
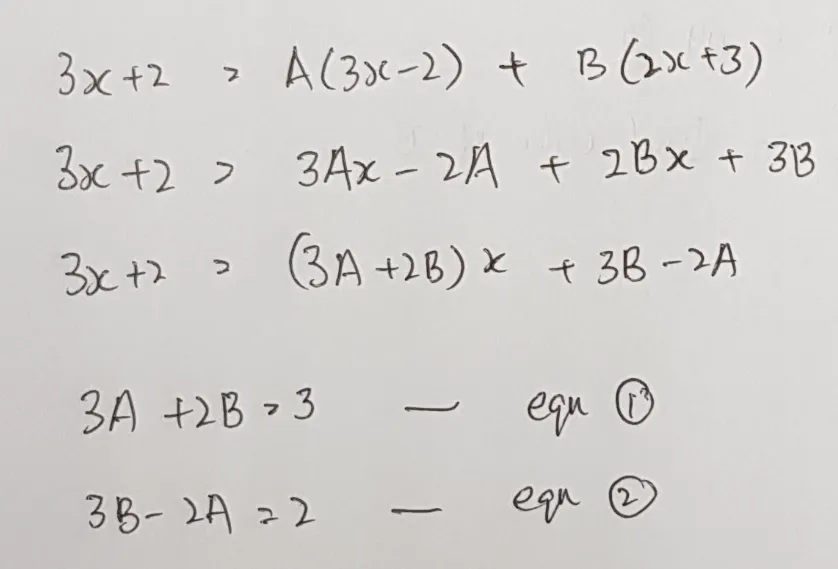
然后,为了得出未知数A和B的值,我们必须先找出其中一个(A或B)的值出来,首先就拿方程式1来开刀吧。
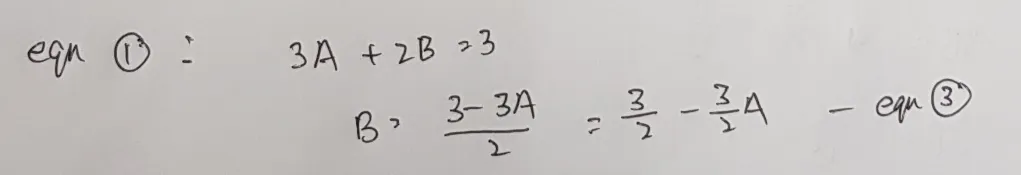
再来个移形换位,我们得到方程式3。
然后我们把方程式3代入方程式2,就会得到A的值,也就是5/13,如下图。
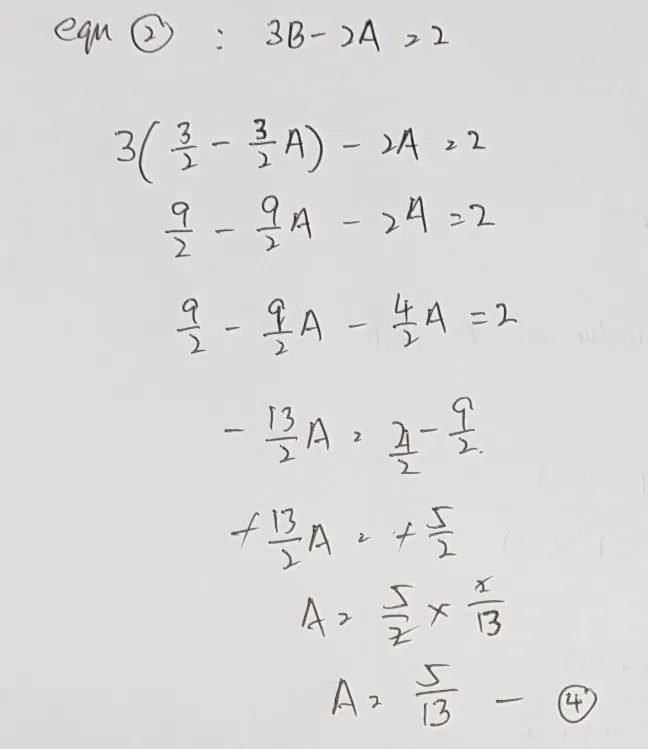
然后再把A的值代入方程式2得出B的值(下图),最后B的值为12/13。

最终的方程式为:

那我们现在来求证一下看看这最终方程式对不对吧,首先让x等于0,把x的值代入最终方程式,看看最后等号左右两边的数值是否相同(如下图)。
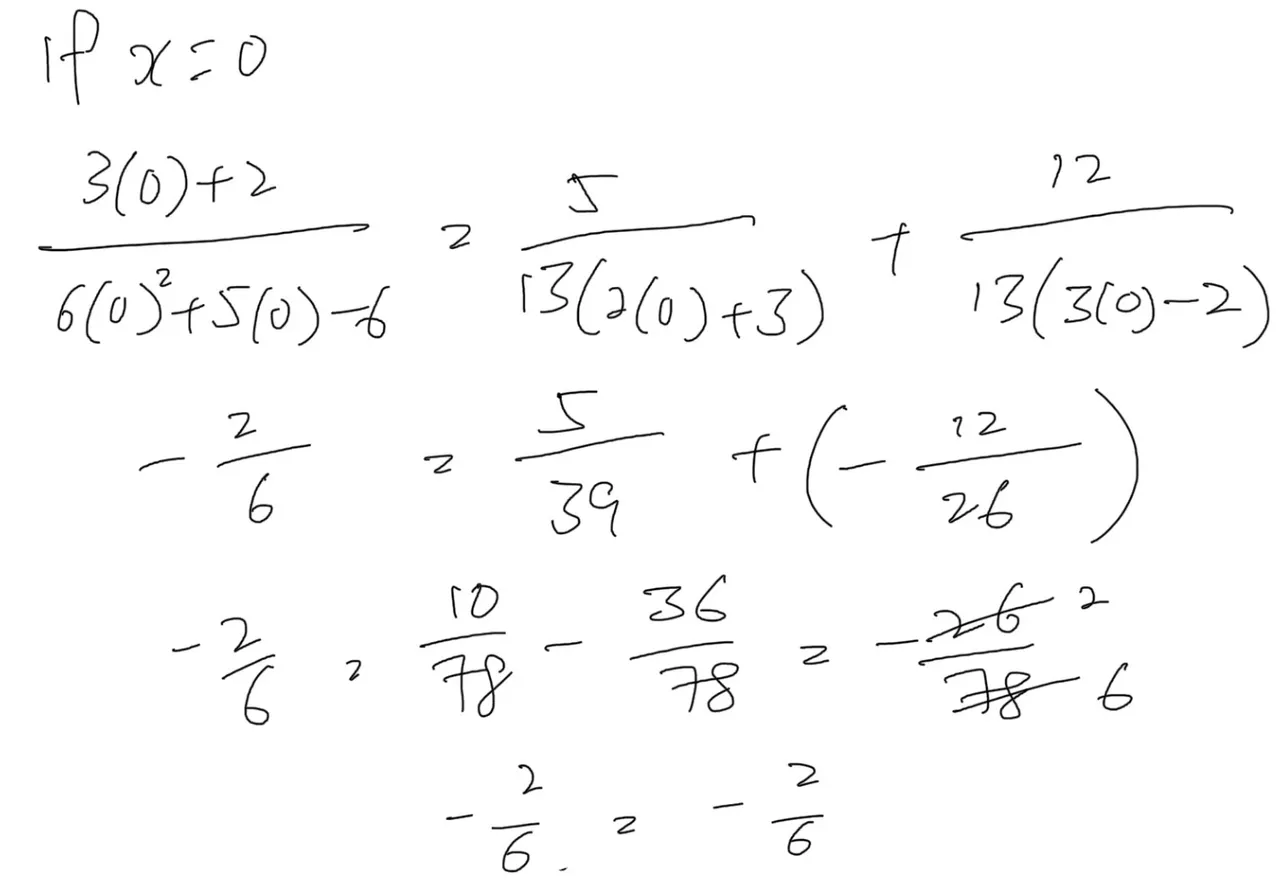
求证成功!两边的数值都一样,证明最终方程式是对的。
最后给大家看一看完整的解答方式吧。



为他人着想
英文有一句谚语(idioms)叫作:Put oneself in someone’s shoes 或put myself in someone’s shoes,意思就是为他人着想。通常英文的谚语都比较直白,就好像刚刚说的这个,把自己放在别人的鞋子里,就是说要站在别人的立场想,用别人的角度看东西,才能了解对方在想什么,才能体谅对方。
其实代数也是一样,多数时候为了求解,我们必须吧一些未知数化成不一样的方程式,再代入其他的未知数来求出其中一个未知数的值,才能找到其他的未知数的值。这就跟做人一样,不管我们做什么事情,我们都必须把自己代入其他人的鞋里,站在对方的立场想一想,看看我们做的东西会不会影响到他人,才能够体谅人。
结语
我们做人,有时候并不能自私,不能为了自己的利益而罔顾他人,就好像是我们不能随便把车停在消防栓附近,万一那里不幸发生火灾的话,这样一来我们不就影响了消防员救人了吗?那我们不就成了帮凶了?所以说我们不能那么自私,总得为别人着想的。
PS: 终于码出了一篇STEM文章了,我的字写的有点丑请多多包涵啊。最后感谢大家的阅读,感恩感恩。
部分内容参考自:
Partial Fraction Decomposition-Wikipedia
部分分式分解-维基百科