
图1:阿基米德像,作者:cheva
一、阿基米德和《羊皮书》
阿基米德是古希腊著名的科学家,生活在希腊在意大利的殖民地叙拉古。大家都熟悉他在洗澡时灵光乍现,想出了如何称量王冠确定确定含金量的故事。其实他还是一个和达芬奇类似的工程师,在帮助自己的城邦抵御罗马人的进攻时,他制作了许多前所未见的战争机器,比如利用杠杆原理掀翻罗马战舰的机器。利用镜面反射聚焦太阳光点燃罗马战舰等等,给攻城的罗马军团造成巨大伤亡。但最终强大的罗马军团还是攻陷了叙拉古,阿基米德也在城破时被乱兵所杀。据说,罗马将军其实很敬重阿基米德的才学,他让士兵去把他请来,当士兵找到阿基米德时,他正在研究一个几何学问题,他要求等他把问题算完再走。粗鲁的罗马士兵认为他在藐视强大的罗马军团。一怒之下杀死了阿基米德。阿基米德死后,他的著作大多散失,留存于世的只有区区八篇文章。
然而在1998年,一部神秘的羊皮书出现在索斯比拍卖行,表面上看这是一部写满基督教祈祷文的手抄本,作者是中世纪拜占庭帝国的一个不知名的教士。但起拍价却高达80万美元。原来,人们发现那个教士是在“废物利用”,这部祈祷文原本是另一本书,那个传教士可能是纸不够用了,于是将原来的文字刮掉,重新写上了赞美上帝的话。而现在人们从残存的笔迹上发现,原书正是阿基米德的著作。
如此重大的发现,甚至惊动了希腊政府,他们派出专员前往拍卖现场,誓要将这国宝拿下。但拍卖当天一位神秘的富豪B先生出手不凡,将价格叫到了200万美元,希腊政府再也无力加价。有猜测说这位神秘的B先生是比尔盖茨。但事实并不是。
神秘的B先生入手后,将“阿基米德白皮书”转而借给多家著名研究机构,并提供经费,要求复原被刮掉的阿基米德原著。经过科学家的不懈努力,真的复原了原书的绝大部分内容,人们惊奇的发现这部抄本不仅包括现存的全部八篇阿基米德的著作,还包括两篇世人从未见过的文章《方法论》和《十四巧板》。其中《方法论》中有许多关于极限的超前思考,可以看作微积分思想的萌芽。下面我们就通过阿基米德计算球体体积的方法来一窥天才的思想。
二、阿基米德计算球体体积的方法
阿基米德关于杠杆原理有一句名言就是“给我一个支点,我可以撬起地球”,他在证明球体体积时,也用到了杠杆原理。如下图:
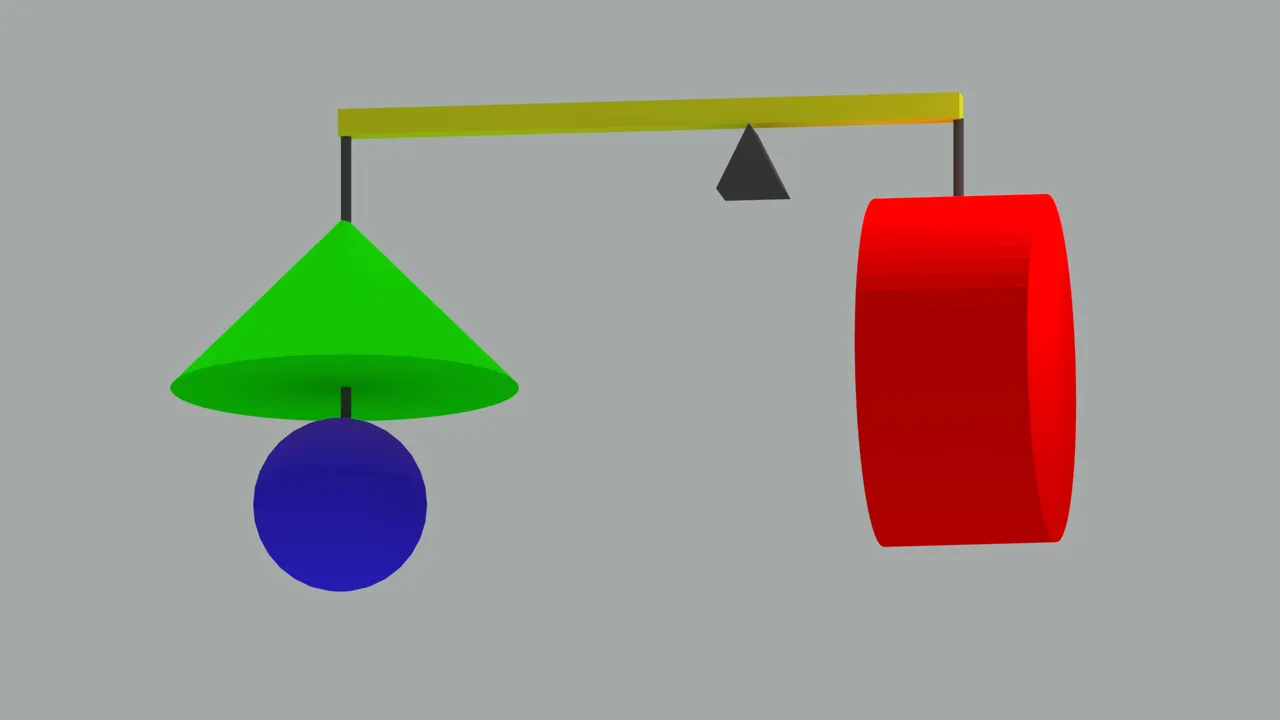
图2:计算球体体积的杠杆配置 作者:cheva
简单说,就是当有一个杠杆,一边挂一个底面半径为2R,高为2R的圆锥和一个半径为R的球体,另一边挂一个底面半径为2R,高也为2R的圆柱。且圆锥与球一侧的力臂为2R,圆柱一侧力臂为R时。假设圆锥、球、圆柱三者材料相同,也就是密度相同,则此时杠杆刚好平衡。
如果三者材料密度相同,则三者所受重力仅与自身体积V相关,根据杠杆原理有:
(V圆锥+V球)×2R=V圆柱×R (式1)
只要证明上述等式即可求出球的体积。当然,你可以通过做实验去验证这个表达式。但在思维发达,逻辑严密的的数学家眼里,做实验这种方法实在登不上大雅之堂。我们看看阿基米德是如何推导的。

图3 作者:cheva
如上图,我们将圆锥、球体和圆柱叠放在一起,从侧面看过去,然后从三个物体上面距左侧x的地方取厚度为dx的薄片(dx很薄,薄到厚度可以忽略不计),即红色部分。因为dx很薄,薄片的体积可以近似应用圆柱体的体积公式,这已经是微分的思想了,即:
因为圆锥的高和底面半径都是2R,所以圆锥横截面是底角为45度的等边直角三角形。所以,截面的半径也等于x,所以有:
V圆锥薄片=πx2×dx
球体截面半径为图中的AB,根据勾股定理可以计算,所以:
V球体薄片=π(R2-(R-x)2)×dx
柱体薄的体积为:
V柱体薄片=π(2R)2×dx
根据杠杆原理:
(V圆锥薄片+V球体薄片)×2R=V柱体薄片×x
约去dx,得:
(πx2+π(R2-(R-x)2)×2R=π(2R)2×x
化简,得:
4πR2x=4πR2x
所以,当从距离左侧x处取一段薄片的体积都能使杠杆平衡。因为x是任意的,也就是说,把三个物体切成许多薄片,每个相应距离的薄片都能使杠杆平衡,则作为整体,圆锥,球和圆柱也能使杠杆平衡,所以(式1)成立。这已经很接近积分的思想了。
根据圆柱与圆锥的体积公式可以算出,球的体积公式:
V球=(V圆柱-2×V圆锥)/2
V球=4/3 πR3
参考资料
- 李永乐老师Youtube频道:数学家阿基米德的羊皮书是如何重见天日的?李永乐老师讲球的体积公式如何推导
- 《阿基米德羊皮书》背后的科学史奇案作者:江晓原
- Archimedes' Method for Computing Areas and Volumes - Cylinders, Cones, and Spheres 作者:Gabriela R. Sanchis
- Volume of Sphere/Proof by Archimedes