0.999...是小于1还是等于1,不知你仔细思考过这个问题没有,我也有段凭直觉想当然的时期认为,0.999...是无限逼近于1,但永远不会到达1。所以,它终究是小于1的。但真的是这样吗,其实数学讲的是逻辑,而不是直觉,有许多方法证明0.999...就是1。
方法1:
这是最简单的方法。
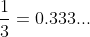
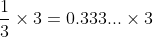
所以
1=0.9999....
方法2
利用等比数列求和公式,其中0<q<1:
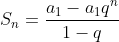
当n趋向无穷大时,a1qn的值趋于0,所以:
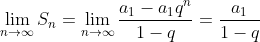
上面就是无穷等比级数的求和公式,而:
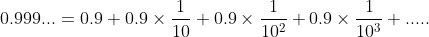
带入无穷等比级数求和公式:
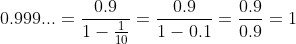
以上是用初等数学证明0.9999...=1,还有更高级的方法来证明,比如用集合论的理论。
我觉得这个问题其实跟古希腊数学家提出的芝诺悖论是一回事,就是一支箭要射中靶子,它必须飞过与靶子间一半的距离,然后又要飞过剩下路程的一半,然后一半又一半。。。这个过程可以无限进行下去。最后得出结论,这支箭永远不会射中靶子。事实上这是不可能的。箭肯定会射到靶子上,所以0.9999...也就等于1。