As part of the Gridcoin Research 4.0 Roadmap (starting here and continuing in a number of other posts), members of the community have proposed to redesign the calculation of magnitude, replacing Recent Average Credit (RAC) with Total Credit Delta (TCD). A big motivation for doing so is the fact that RAC is complicated to calculate, even under the simplest possible assumptions (for details, see this post and references). This has lead to frustration in terms of estimating rewards. On the other hand, TCD is much simpler: it is just the difference in a user’s credits earned on a specific project between superblocks.
The community has already voted to replace RAC with TCD. So what’s my goal here? Well, I want to try my hardest to ‘poke holes’ in either metric and see what ‘exploits’ I can find. This will help us know how to securely transition from RAC to TCD, and also function a sanity check to make sure TCD does what we really want it to.
IF you are busy and don’t have time to read this (somewhat technical) post, that’s ok. Just bookmark it as something to reference when RAC and TCD come up again in future discussions. If you have enough time though, then great – read on!
This post will be the first in a short series of ‘case studies’ each looking at potential ‘exploits’. Let’s begin…
Case study 1: Distribution in time

Scenario A. Suppose you have a GTX 1080. You’re crunching Einstein@home. Would it increase earnings to 'save up' completed workunits and submit all at once? Or send them in as they are completed? In other words, does it help to strategically 'spike' your RAC?
Scenario B: The same idea as in A. Would it increase earnings to crunch intensely on project X for 1 day, switch to project Y and crunch again for 1 day, then project Z, etc. ? Or stick to the same project?
Scenario C. Suppose you can rent a huge computing cluster for some $ / (FLOPS * unit time). Is your profit margin maximized by crunching super intensely for 1 day ('spiking')? Or distributing the crunching over time? Admittedly, this case is a little artificial, since if mining is profitable you’d want to crunch as much as possible anyways. But let’s suppose you’re right on the margin of profitability. Could crunching super intensely all at once push you from loss and into profit? Or perhaps the cluster is under high demand, so that, for instance, you can only choose one of the two: 1) Crunching at X FLOPS for 1 day, or 2) Crunching at X/30 FLOPS over 30 days. Is option (1) preferable?
Some simplifying assumptions: First, the number of whitelisted projects does not change. Next, the network RAC (call it ‘R_total’) for your chosen project is fixed: R_total = constant. I’ll call your own RAC on the ith day ‘R_i’, starting at i = 0. Let’s also assume RAC is updated daily, and your initial RAC is 0: R_0 = 0.
In terms of these quantities, what are your total earnings? Well, let’s say superblocks arrive daily. Then we should have:
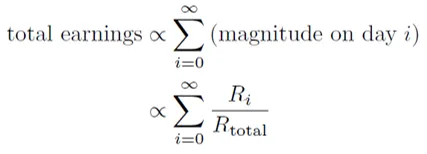
I'm skipping over the technicalities behind actual distribution of rewards, RSA, research age, and all that. Those are quantities I admittedly don't understand 100%. Nevertheless, I hope the above equation for the total earnings is mostly correct, even if the actual rewards distribution over time is more complex.
Now, let’s say you earn X_1 credits on day 1, X_2 credits on day 2, and X_3 credits on day 3. We will assume this is all the crunching you do, although the conclusions that follow will hold regardless of how many days you crunch. Our initial questions now boil down to a mathematical statement: For fixed total credits, X_1 + X_2 + X_3 = constant, does the distribution over X_1, X_2, and X_3 matter?
Answer: No. I'll sketch the steps in the proof. Let r = 1 - 2^(-1/7) = 0.09428… Using the results from here and here, and assuming time is given in units of days, we have
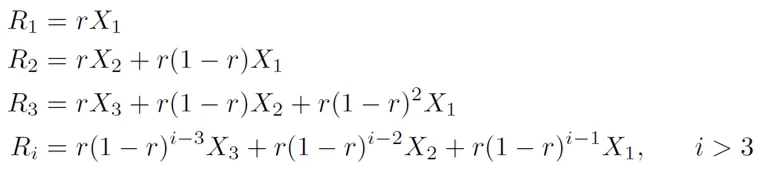
Great. Now let’s add everything up:

In the second step I have assumed R_total does not depend on i. Under these circumstances, then, it indeed doesn't matter how you distribute your credits. There is one rather obvious caveat, however: R_total does depend on i:
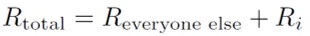
i.e. you are competing with yourself. For small R_i this doesn’t matter, and our previous result holds to a very good approximation. But for large R_i you definitely get better earnings by distributing resources equally across time and projects. This issue was touched on in this post. Top miners, take note!
Now I want to argue that this is actually a good feature. We want the top miners to distribute their resources consistently across time and uniformly across projects. This makes for a more robust network.
In a similar vein of thought, I want to argue that fluctuations in 'R_{everyone else}' are not problematic. This is because 'R_{everyone else}' functions sort of like the 'difficulty' in ordinary hash mining. Just like difficulty regulates how often blocks are mined, 'R_{everyone else}' regulates the mining power devoted to a project, as miners look to where they can maximize profits. So this extra variable shouldn't bother us at all.
That’s it for RAC. How about TCD? I think it should be fairly obvious that exactly the same conclusions hold for TCD. So in the transition to TCD, we shouldn’t have to worry about unfair distribution of resources to maximize rewards. I apologize if this was already obvious to some people. But it’s good to have down on paper. In the next couple posts I’ll look at more interesting ‘case studies’, where RAC and TCD are in fact different in their outcomes. Stay tuned.
One final note. This analysis is done at an abstract and simplified level. In reality, the behavior of RAC is a huge mess, due to a variety of uncontrolled variables; see the posts by @jefpatat on this topic (starting here). Just another reason to get rid of RAC and move to TCD!