Das Rätsel der 100 Gefangenen

Liebe Leute,
die Lösung dieses Rätsels ist so einfach wie genial, dass ich es mit Euch teilen muss!

Folgende Aufgabe:

• Es gibt 100 Gefangene, die von 1 bis 100 durchnummeriert sind.
• In einem Raum stehen 100 Boxen, in denen zufallsartig Zettel mit den Nummern von 1 bis 100 sind.
• Jeder Gefangene darf 50 Boxen in dem Raum öffnen um zu schauen, ob in einer davon seine eigene Nummer ist. Danach muß er den Raum verlassen, ohne irgendetwas geändert zu haben, und er darf danach auch nicht mit den anderen Gefangenen kommunizieren.
• Bevor der 1. Gefangene den Raum betritt, dürfen sie aber ihre Vorgangsweise besprechen.

Etwas schematisch kann man sich das so vorstellen: Hier macht Gefangener #1 gerade seine 50 Boxen auf und hofft, dass er eine "1" findet.



Es geht um Leben und Tod, denn nur wenn ALLE 100 Gefangenen ihre eigene Nummer finden, werden alle freigelassen. Falls auch nur ein einziger seine Nummer nicht findet, werden alle exekutiert.

Was ist die beste Strategie?

Anmerkung:
Wenn jeder der 100 Gefangenen wahllos 50 Boxen untersucht, ist die Wahrscheinlichkeit, dass alle ihre eigene Nummer finden genau 0,5¹⁰⁰, das ist 0,0000000000000000000000000000008, also quasi 0!

Es gibt aber eine (wenn man es weiß) simple Methode, um ihre Überlebenschance drastisch zu erhöhen!
Eure Gehirnzellen sind jetzt gefragt! Googlen unerwünscht!

Findet jemand die Lösung?

^{made with MidJourney}

---

EDIT: Die Lösung

Das Verfahren ist denkbar einfach. Jeder Gefangene öffnet (und dass muss vorher besprochen und durchgezogen werden) zunächst die mit seiner Nummer beschriftete Schachtel. Falls die Box seine Nummer enthält, kann er gehen und der nächste Gefangene ist dran. Andernfalls fährt er fort und öffnet die Schachtel mit der Nummer, die in der letzten Schachtel gefunden wurde. Das Verfahren wiederholt sich, bis der Sträfling entweder seine Nummer findet oder die 50 Versuche aufgebraucht sind. Mit dieser Vorgangsweise können die Gefangenen ihre Überlebenswahrscheinlichkeit auf 30% erhöhen, was um Etliches besser ist als 0,5¹⁰⁰.

Aber wieso funktioniert das?

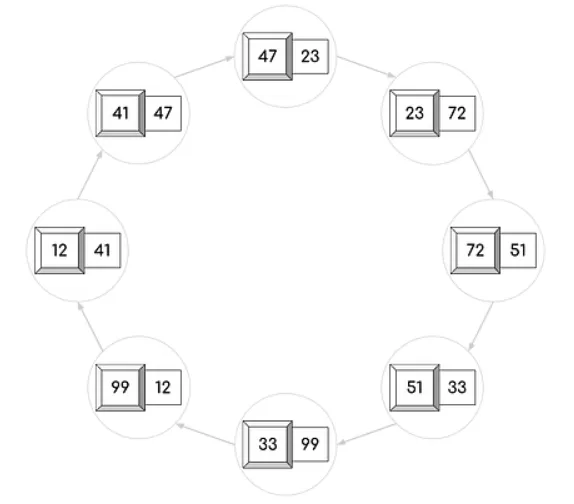
Letzlich hat der Gefängniswärter nichts anderes gemacht, als die Zetteln mit den Nummern in den Boxen vertauscht, also permutiert. Dadurch entstehen einer oder mehrere Kreise von Zetteln wie in diesem Beispiel:

https://ichi.pro/de/eine-verstandliche-erklarung-zur-losung-des-100-gefangenen-ratsels-267205639256772

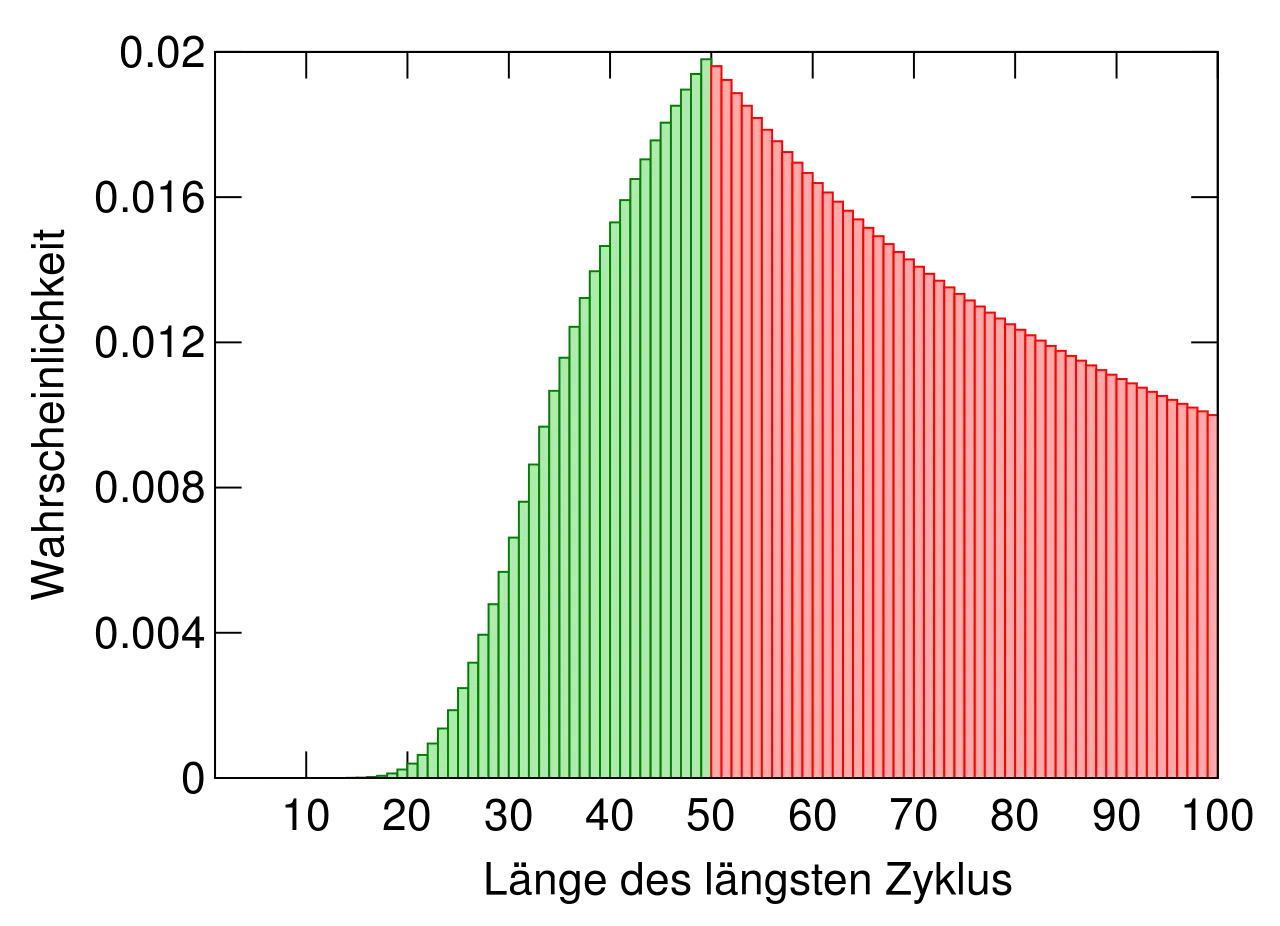
Durch ihre Vorgangsweise folgen die Gefangenen jeweils diesen zyklischen Permutationen anhand der Schubladenzahlen und den darin liegenden Zetteln. Solange kein Zyklus länger als 50 ist, haben alle Teilnehmer ihre Nummer spätestens mit der 50. Schublade gefunden und werden freigelassen. Falls ein Zyklus dabei ist, der über 50 lang ist, dann funktioniert es natürlich nicht. In dieser Grafik sieht man, wie hoch die Wahrscheinlichkeit ist für Zyklen einer bestimmten Länge, alle grünen sind <=50 und bedeuten Freiheit, sie machen in Summe 30% aus!

https://de.wikipedia.org/wiki/Problem_der_100_Gefangenen#L%C3%B6sung