Ciao a tutti,
oggi sono malata, ma delle mie avventure di oggi ne parlerò domani. Ad ogni modo oggi voglio mostrarvi come creare i triangoli di Sierpinski. Wacław Sierpiński era un matematico e per la prima volta nel 1915 ha descritto la seguente figura:

Devo ammettere che non sono una matematica, quindi @CharlesX cerca di perdonarmi. Ricordo a tutti che programmo per diletto e quindi sicuramente un professionista avrebbe fatto meglio di me. Fatto il doveroso bagno di umiltà cominciamo...
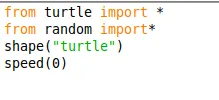
Importiamo per prima cosa il modulo turtle e poi quello random. Useremo poi questi due moduli, ma per ora usiamo il comando shape("turtle"): con questo comando diciamo che il cursore assumerà la forma di tartaruga. Con il comando speed(0) assegniamo la velocità massima per disegnare alla nostra tartaruga.

Definiamo la funzione Sierpinski. Questa funzione dipende da:
✅ Lunghezza_dei_lati: cioè dalla lunghezza dei lati del triangolo;
✅ RT: cioè la profondità di iterazione;
✅ colore.
Per quando riguarda il parametro RT dal suo valore dipende il numero di triangoli creati.
🔶 Per RT pari a 1 avremo 3 triangoli; ⇨ questo è il livello 1 di ricursione.
🔶 Per RT pari a 2 avremo 3⋅3=9=32 triangoli; ⇨ questo è il livello 2 di ricursione.
🔶 Per RT pari a 3 avremo 3⋅3⋅3=27=33 triangoli; ⇨ questo è il livello 3 di ricursione.
🔶 Per RT pari a 4 avremo 3⋅3⋅3⋅3=81=34 triangoli; ⇨ questo è il livello 4 di ricursione.
Il triangolo di Sierpiski ha un livello di ricursione 6 quindi si creeranno 36 triangoli.
Dopo aver creato la funzione iniziamo a colorare i triangoli che poi disegneremo con begin_fill(). Affidiamo alla variabile colore il valore color, e poi andiamo a definire color. Quest'ultimo avrà valori random per tutti e 3 i colori principali usati da Python: il rosso, il blu e il verde.
Usiamo il ciclo for iterando una rotazione a sinistra di un angolo pari a 120° per ben 3 volte.

Iniziamo un ciclo if valido quando la RT, cioè il nostro livello di iterazione sia superiore a 0.
- Richiamiamo la funzione Sierpinski con Sierpinski(Lunghezza_dei_lati/2, RT-1,color) con parametri pari a metà della lunghezza dei lati: cioè Lunghezza_dei_lati/2, livello di iterazione RT-1 e color (random). Verrà così disegnato il primo triangolo a sinistra in basso.
- Avanziamo di un valore pari a Lunghezza_dei_lati/2 con il comando forward(Lunghezza_dei_lati/2). Andiamo quindi a metà del nostro lato.
- Richiamiamo la funzione Sierpinski con Sierpinski(Lunghezza_dei_lati/2, RT-1,color)
Verrà così disegnato il secondo triangolo a destra in basso. - Torniamo indietro di un valore pari a Lunghezza_dei_lati/2 con il comando backward(Lunghezza_dei_lati/2).
- Effettuiamo una rotazione a sinistra di un angolo pari a 120° con left(120).
- Avanziamo di un valore pari a Lunghezza_dei_lati/2 con il comando forward(Lunghezza_dei_lati/2).
- Effettuiamo una rotazione a destra di un angolo pari a 120° con right(120).
- Richiamiamo la funzione Sierpinski con Sierpinski(Lunghezza_dei_lati/2, RT-1,color)
Verrà così disegnato il terzo triangolo in alto. - Effettuiamo una rotazione a sinistra di un angolo pari a 120° con left(120).
- Torniamo indietro di un valore pari a Lunghezza_dei_lati/2 con il comando backward(Lunghezza_dei_lati/2).
- Effettuiamo una rotazione a destra di un angolo pari a 120° con right(120).
NB: I comandi dal punto 4 al punto 7 (4-7) sopracitati servono per spostare la tartaruga a metà del lato sinistro inclinato.
Ora bisogna vedere cosa faremo quando arriveremo al livello 0 di iterazione.

Nel caso in cui fossimo arrivati al livello 0 di iterazione: disegniamo semplicemente l'ultimo triangolo e fermiamo il processo. Per questo scopo, ovvero per disegnare l'ultimo triangolo utilizziamo un ciclo for che itererà, cioè ripeterà, le stesse operazioni 3 volte. Le operazioni sopracitate sono:
🔶 Avanziamo di un valore pari a Lunghezza_dei_lati/2 con il comando forward(Lunghezza_dei_lati/2).
🔶 Eseguiamo una rotazione a sinistra di un angolo pari a 120° con left(120).
A questo punto possiamo finire di colorare con end_fill() avevamo iniziato a disegnare non appena definita la funzione Sierpinski (vedi prima foto del programma).
Definiamo in concreto la funzione Sierpiski in questo modo: Sierpinski(300,6,color). Il parametro Lunghezza_dei_lati sarà pari a 300 pixel, la profondità di iterazione 6 e il colore sarà uguale a color, permettendo così al programma di scegliere colori random.
Per chiarire meglio il funzionamento ho preparato un video:
Il programma lavora per RT pari a 6. Proviamo a vedere il risultato per RT pari a 1:

Al livello 1 troviamo 3 cioè 31triangoli colorati.
Proviamo a vedere il risultato per RT pari a 2:

Con il livello 2 di iterazione troviamo 9, cioè 32 triangoli colorati.
Proviamo a vedere il risultato per RT pari a 3:

Con il livello 3 di iterazione troviamo 27, cioè 33 triangoli colorati.
Proviamo a vedere il risultato per RT pari a 4:

Con il livello 4 di iterazione troviamo 81, cioè 34 triangoli colorati.
Proviamo a vedere il risultato per RT pari a 5:

Con il livello 5 di iterazione troviamo 243, cioè 35 triangoli colorati.
Il nostro programma aveva livello 6 di iterazione, sono dunque stati creati ben 729 ovvero 36 triangoli colorati. Per vedere quanti triangoli sono stati creati andate al video di sopra: Il triangolo di Sierpinski/Sierpinski triangle
Grazie di avermi seguita...
Alessandra
PUNTATE DI PYTHON:
➤ Il Python e le tartarughe.
➤ Python e le bandiere.
➤ 🍀🍀 Triangoli e quadrifogli con Python.🍀🍀
➤ I cerchi con Python.
➤ I fiori con Python.
➤ Modelliamo un mondo astratto con Python.
➤ Compito risolto di Python.
➤ Sole, luna, stelle: alla conquista dell'universo!!!
➤ Pentagoni ripieni con Python.
➤ ⭐⭐Le galassie con Python.⭐⭐
➤ Cono stradale multicolore con Python.
Dove non diversamente indicato le foto sono di mia proprietà