지난 포스트에서는 블랙홀의 이론적 배경에 대해서 간략히 알아보았다.
현실 세계(?)에서 블랙홀은 어떻게 존재하고 관측되는지 알아보고 블랙홀의 생성 과정에 대해서 다루어 보려고 한다. 전에도 이야기 했듯이 블랙홀은 중력이 매우 강해서 빛 조차 흡수한다. 즉 블랙홀의 경우 빛을 흡수하여 전자기파로 인한 관측이 불가능하다. 다만 블랙홀은 강한 중력으로 인해 중력파를 발생하여 블랙홀의 존재 여부를 중력파 관측을 통해 확인 할 수 있다. (LIGO 의 관측들은 블랙홀 (쌍성) 에서 발생한 중력파이다. )
우주의 절반 이상의 별들은 쌍성으로 구성되어 있어, 대부분의 블랙홀들은 쌍성 상태로 존재한다. 이러한 쌍성 블랙홀들을 Binary Black Hole 약자 BBH 로 부른다.
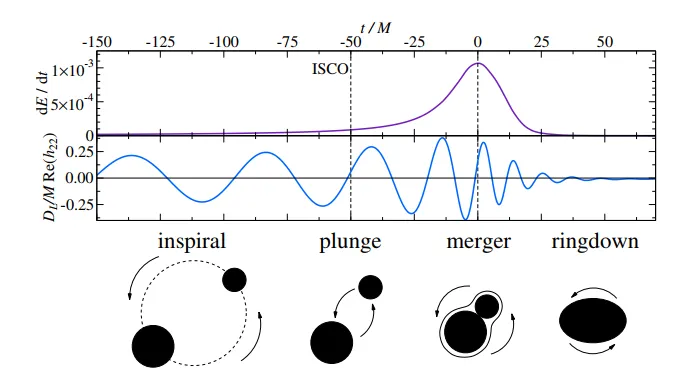
[2014 년 Andrea Taracchini, University of Maryland ; Doctoral Dissertation, 박사 학위 논문의 Fig 2.1 을 참조 ]
이러한 BBH의 생성 과정은 크게는 3단계 (Inspiral-Merger-Ring down) 좀 더 자세히는 4단계 (Inspiral- Plunge - Merger - Ring down ) 으로 기술된다. 이중 특별히 Inspiral 과 Ringdown 을 설명하는 이론들은 잘 정립되어 있으나 Merger 부분에서는 특별히 잘 맞는 이론이 없어 주로 수치중력 방법을 이용하여 계산을 한다. 위의 그림을 통하여 직관적으로 어떤 상황인지 쉽게 이해 할 수 있을 것이라 본다.
Inspiral 의 경우 궤도가 점차 나선형을 이루며 줄어들면서 가까워 지는 상태를 말하며, 뉴턴 역학의 이론을 적용하여도 어느정도 잘 맞는다. 더 나아가 Post-Newtonian approximation이라는 방법을 이용하면 (0PN=Newtonian, 1PN, 2PN, 3PN,.. 까지는 잘 알려져 있고 현재 4PN 에 대한 연구들이 진행 중이다) 더 정밀하게 현상을 이론적으로 설명 할 수 있다.
LIGO LAB Caltech:MIT - Spiral 에 대한 이해를 위해 유투브 시물레이션 영상을 첨부한다.
이후 두 물체가 가장 안정된 원형 궤도에 도달했을 때(ISCO- innermost stable circular orbit 의 약자)를 Plunge 라 하고 이 후 두 물체가 합쳐지는 Merger 단계에 돌입한다. 이 단계의 경우 특별히 이 단계를 잘 기술하는 이론이 없어, 수치 중력의 다양한 방법론을 (수치 중력은 또 하나의 학문이 될 정도로 엄청나게 큰 분야이다, 전에 포스트에서도 이야기 했듯이 아인슈타인의 장 방정식은 비선형 방정식으로 exact solution 을 쉽게 구할 수 없다. 또한 편미분 방정식을 정확하게 기술하기 위해서는 미분방정식의 초기값이나 경계값 문제 등 을 고려해야 한다. 이러한 여러가지 상황을 수치 중력 이론들 (가장 유명한 방법이 ADM 방법이다)은 각각 상황에 맞게 물리적 조건을 취해가면서 컴퓨터 시물레이션을 통해 해결한다.) 통하여 엄청난 시물레이션을 통해 어떤 현상의 이론적 모델을 유추하고 있다. 이 Merger 단계에서는 gravitational luminosity가 최대가 된다. (첫번째 diagram 의 보라색 peak 참조) - 즉 이 때 중력파를 가장 많이 발생한다.
LIGO LAB Caltech:MIT - 블랙홀의 merger 과정을 보여주는 유투브 시물레이션 영상을 첨부한다.
이후 Ring down을 거쳐 안정화가 되는데 이 Ring down 에서부터 일반적인 BH perturbation 을 계산을 통해 Quasi-normal mode 를 탐지 할 수 있다.
중력파 자체만을 가지고도 상당히 공부할 거리가 많다. 관측 할만한 크기(?), 규모의 중력파는 블랙홀 생성과정 말고도 여러가지 있다. 또한 중력파 자체와 관련된 수학적 물리적 응용 또한 현재 진행중인 연구 과제이다. 중력파의 이론적 모델에 대해서 가장 잘 알려진 이론은 Linearized perturbation 이론으로 curved metric 을 Minkowski metric (flat ) 와 small perturbation 으로 분해하여 전개하는 근사 이론이다. 간략히 수식을 써보면
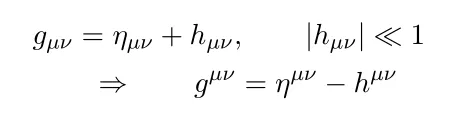
이 metric 을 이용하여 Christoffel Connection, Riemann tensor 등을 계산 할 수 있으며 이를 통해 아인슈타인의 장 방정식의 좌변 성분인 리치 텐서와 리치 스칼라를 구할 수 있다.
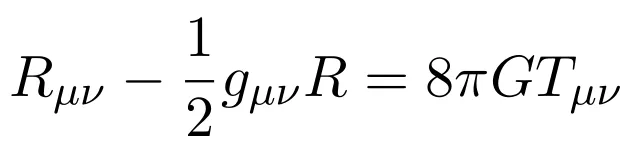
특정한 게이지 조건을 이용하여 아인슈타인의 장 방정식을 small perturbation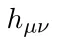 
에 관한 방정식으로 변형하여 이 
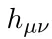의 해를 구할 수 있고 이 해가 중력파를 기술한다. 중력파의 자유도는 (10-4-4=2) 2개로 +, x polarization 이 있다. (일반적인 D dimensional spacetime 에서 graviton 은 D(D-3)/2 만큼 자유도를 갖는다. 여기서는 4차원 중력을 다루어 2개의 자유도가 있는 것이다. 재밌게도 3차원 중력의 경우 이러한 자유도가 없다. 다른 차원에서의 중력은 또 다른 재미있는 공부거리이다)
왜 +, x polarization 이라 하는지는 위 그림을 보면 이해가 될 것이다. [사진 위키 참조]
수학적으로도 중력파는 harmonic gauge, Einstein equation 의 솔루션 분석 등 상당히 많이 연구되고 관심받는 분야이다.
더 자세한 이야기를 하고 싶은데 육체적 정신적 피로로 인하여 오늘은 여기서 마무리를 하려고 한다. 위 과정, Linearized gravity 에 대한 자세한 내용은 다음에 기회가 되면 다루도록 하겠다. Modifed gravity 이론들 (대표적인 예로 f(R) gravity) 도 할 이야기가 상당히 많다.
일단 다음 포스팅, 이번 주제 관련 대중과학서(?) 를 소개를 끝으로 이 주제를 마무리 하려고 한다.
1, 3 부 포스팅
[과학] 중력파와 블랙홀-1 [이론소개 중심]
[과학] [과학, 책] 중력파와 블랙홀-3 [관련 도서/자료(?) 소개]]