勾股定理,大家初中就学过。勾股定理在西方叫毕达哥拉斯定理,说的就是在直角三角形中,两个直角边的平方和等于斜边的平方。如果用x和y分别表示两个直角边的长度,用z表示斜边的长度,那么勾股定理可以表示成:
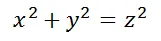
这个代数方程看上去简单明了,那么如果我们在它的基础上推广一下,会得出什么结论呢?
首先,如果把平方推广到n次方,那么就有下面这个方程:
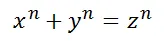
如果n = 2,那么这就是勾股定理。在n = 2的时候,这个方程是有正整数解的。比如3,4,5就是一组勾股数,也就是 32 + 42 = 52。那如果在n > 2的情况下,我们要问的问题是:这个方程还有正整数解吗?答案是没有,不信你自己试试。
当n > 2时,xn + yn = zn 没有正整数解。这个命题看上去很普通,可实际上却一点也不普通。这个命题最早在17世纪由费马提出,历经了三百多年可一直没人能够证明。最终在1995年才被彻底证明,这就是著名的费马大定理。费马大定理的证明过程就不在这里讨论了。花费了人类三百多年才证明出来的定理,证明过程肯定不简单啦。
除了从勾股定理推广到费马大定理以外,回到直角三角形本身,我们还能推广出啥来呢?要不咱看看两个直角边的平方的倒数的和有什么性质吧 。
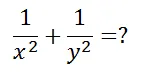
这个问题的答案是:
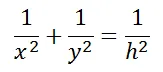
h是直角三角形斜边上的高。证明起来也很简单:
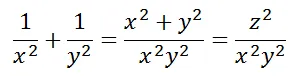
对直角三角形来说,面积既可以写成两个直角边乘积的一半,也可以写成斜边和斜边上的高的乘积的一半。所以我们就有:
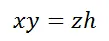
所以:
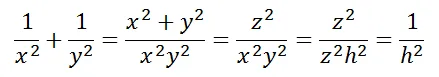
这样我们就把这个命题证明完毕了。虽然这个证明的过程比较简单,但我们从中可以看出数学就是这么奇妙。我们从一个简单的勾股定理,就能推出来这么多有趣的性质,是不是让人觉得很有意思呢?
Reference
Posted from my blog with SteemPress : http://softmetal.vornix.blog/2019/02/05/%e4%bb%8e%e5%8b%be%e8%82%a1%e5%ae%9a%e7%90%86%e6%8e%a8%e5%b9%bf%e5%8e%bb/