Saludos cordiales...

Antes de comenzar a leer esta publicación es recomendable revisar mis dos entregas anteriores, con la finalidad de hacer un seguimiento del tema y obtener una mejor compresión del mismo.
En esta ocasión hablare sobre una herramienta fundamental en el área de los semiconductores como lo es el efecto Hall.
La caracterización eléctrica de materiales se han convertido en un estudio esencial para los materiales semiconductores, ya que esto nos da una idea de la aplicación que cierto material pueda tener en el ámbito tecnológico. el efecto Hall es un método muy importante para los científicos en la actualidad y forma parte de un estudio indispensable en los laboratorios de semiconductores, debido a la creciente demanda de las industrias por la creación de nuevos dispositivos más eficientes, versátiles, económicos y de alta duración.
El efecto Hall nace de la importancia del estudio de diferentes propiedades eléctricas en un material como; densidad de portadores, resistividad eléctrica, y movilidad de portadores en semiconductores y metales.
Este material se dividirá en 3 publicaciones; la primera compartiré un breve resumen teórico y conceptos básicos sobre el efecto Hall, a su vez como calcular la conductividad, densidad y movilidad eléctrica en una placa semiconductora. La segunda un método del coeficiente Hall. Y por último algunas técnicas de caracterización como la de Van Der Pauw y otras consideraciones acerca de la geometría de la muestra y medidas de resisitividad eléctrica.
Wikipedia dice los siguiente acerca del efecto Hall:
Se conoce como efecto Hall a la aparición de un campo eléctrico por separación de cargas, en el interior de un conductor por el que circula una corriente en presencia de un campo magnético con componente perpendicular al movimiento de las cargas. Este campo eléctrico (campo Hall) es perpendicular al movimiento de las cargas y a la componente perpendicular del campo magnético aplicado. Lleva el nombre de su primer modelador, el físico estadounidense Edwin Herbert Hall (1855-1938).
Entonces un principio fundamental que está involucrado es la fuerza de Lorentz, dicho fenómeno se encuentra ubicado por debajo del efecto Hall, es decir esto sucede cuando un electrón se movilizada dentro del campo eléctrico perpendicular al campo magnético que se aplica, por lo tanto este campo experimenta una fuerza en ambas direcciones que se mueve constantemente como respuesta de la fuerza magnética y la fuerza dentro del interior del campo eléctrico del material.
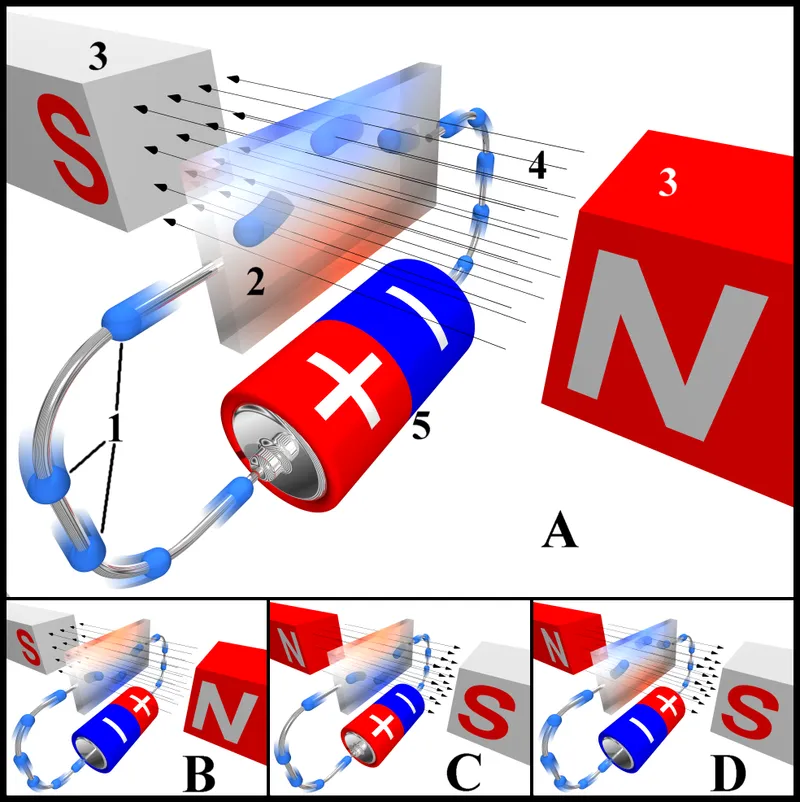
Diagrama del efecto Hall, mostrando el flujo de electrones. Licencia CC BY-SA 3.0 de wikipedia
Este principio físico funciona para cualquier semiconductor, por ejemplo; si tenemos un material semiconductor con tipo de conductividad negativa, sabemos muy bien que por ser tipo n los portadores mayoritarios vendrían siendo los electrones que ocupan una mayor densidad en la muestra. Dicho ero se puede asumir que la corriente que circula dentro de la barra del semiconductor, fluye constantemente en el eje de coordenadas X de izquierda a derecha de un campo magnético Z como se muestra en la figura 1.
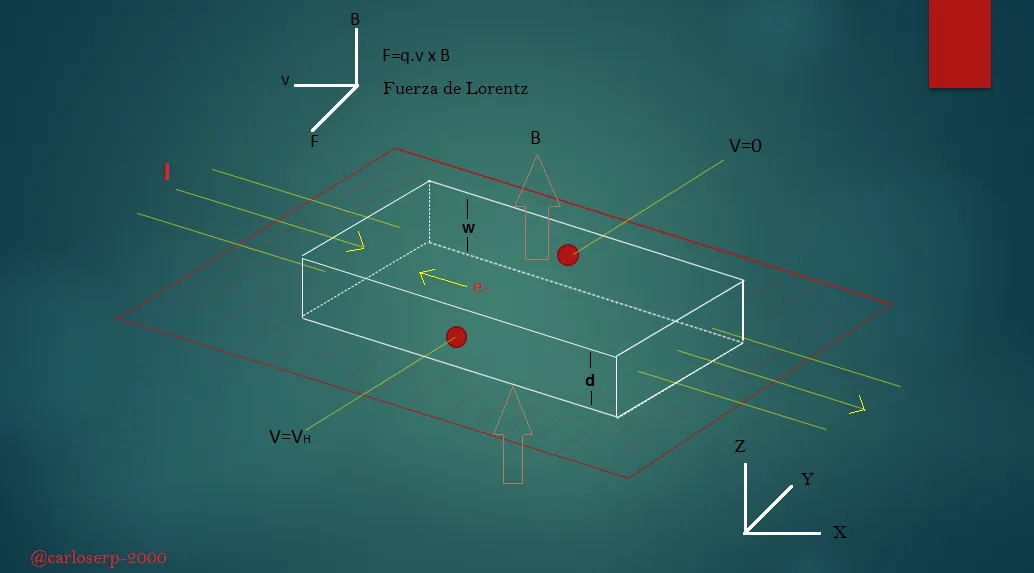
Figura 1. Diagrama del efecto Hall en una barra semiconductora
Ahora bien, si portadores mayoritarios en la barra semiconductora que están sujetos por la fuerza de Lorentz al comienzo se alejan de la corriente que esta dirección hacia el eje Y-, produciendo así un exceso de carga en el material. Si tenemos un desplazamiento limpio de electrones en una dirección y al ser el material cero, debe aparecer una carga limpia igual y opuesta en el otro lado del material semiconductor, dando por consecuencia la aparición de un campo eléctrico EH, y una diferencia de voltaje que se llamara voltaje Hall VH [1-2].
Si tenemos dos cargas continúas separadas, los portadores de cargas libres deben hacer la fuerza eléctrica que se ejerce dentro de un campo eléctrico transversal EH en el material iguala la fuerza de Lorentz, esto se puede observar mediante la siguiente expresión:
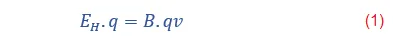
Por otro lado, si en la barra semiconductora denominamos su ancho como "w", las caras opuestas de la barra tendrán una diferencia de potencial VH:
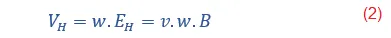
Ahora consideramos la densidad de corriente j ̅ y la velocidad promedio de los electrones o portadores de carga mayoritarios v ̅ mediante la siguiente relación:

Tomando en cuenta que n es la concentración de los portadores de carga.
El voltaje Hall se puede representar mediante la siguiente expresión:
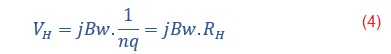
RH es el coeficiente Hall.
Si expresamos la igualdad de la intensidad de corriente I, tenemos los siguiente:
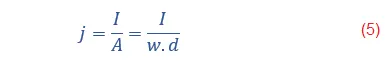

Los portadores se encuentran sometidos por causa del campo eléctrico que se encuentra paralelo a la corriente eléctrica,

Ahora la velocidad de los portadores está dada por la siguiente expresión:
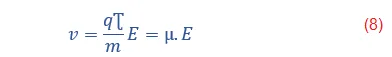

Donde µ recibe el nombre de movilidad de los portadores de carga q y masa m.
Si nos basamos en la famosa ley de Ohm, podemos encontrar la conductividad eléctrica σ en la barra semiconductora por medio de:

Para medidas en función de la temperatura T en un material intrínseco tenemos:
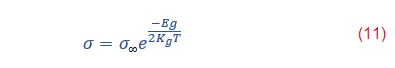
KB: constante de Boltzmann = 8.625x10-5 eV.K-1.
σ∞: conductividad eléctrica a altas temperaturas.
Eg: brecha de energía entre la banda de conducción y de valencia.
Y finalmente luego de desarrollar todo este conjunto de ecuaciones y a partir de la ecuación (11) podemos encontrar el valor real de la conductividad eléctrica de un semiconductor mediante la siguiente expresión:
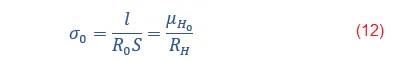
R0: resistencia de la placa.
l: la longitud de la placa.
S: el área de su sección transversal.
y finalmente µHO la movilidad Hall a temperatura ambiente[3].
Y es así como podemos hallar diferentes propiedades eléctricas en una barra semiconductora.
En mi próxima entrega hablare sobre el coeficiente Hall y algunas técnicas de caracterización.
Bibliográficas consultadas
Paginas web

No olvides votar por @stem.witness como testigo

Ahora puedes escribir tus publicaciones a través de la app oficial https://www.steemstem.io y obtendrás un voto extra del 5%