So today, as usual, I was browsing through science posts in steemit and saw a post related to diffusion (and transport) of molecules through the cell membrane by @hadji. So I thought why not just demonstrate how to model diffusion using Random walk? By the way, you can read this post from the link below:
Membrane mediated transportation: Diffusion
I will demonstrate an unbiased 2D(2 - dimensional space) random walk first. Then generalize the code to model diffusion again in 2D space.
Random Walk

In a 1 dimensional case (consider a line), a fair coin toss experiment repeated multiple times can be considered as a 1D-Random Walk process. What does this mean? Fair coin toss gives you tails/heads with equal probability. See the figure below. Let us imagine an entity at origin point 0. We will associate the heads from coin toss as a rightward step and tails as a leftward step. Keep on repeating this experiment. This is an unbiased random walk because the probability to move right or left is 50%.
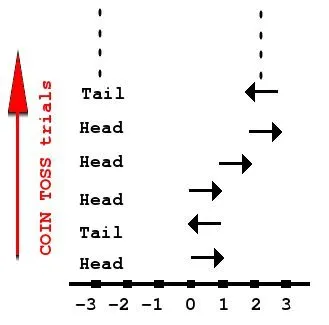
In a 2D case, your origin is a point in the 2D plane. Instead of 2 directions right and left, you need 4 directions. Now you can implement this using a random number generator which produces 4 options in equal probability ie with probability 25%. Like shown below:
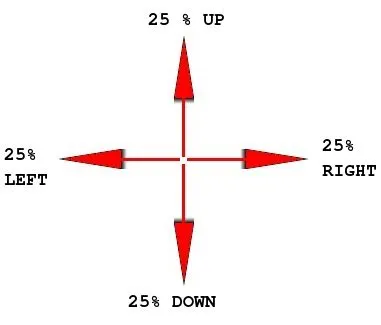
This can be realized using a uniformly distributed pseudo-random number generator. It is easy to realize this in a computer using any programming language. Since I am a lazy guy, I will try MATLAB to implement this.
Algorithm for 2D Random Walk
- Assume a 2D space and place a point on the center of it.
- START LOOP (RUN for say 1000 steps)
a) Generate a Uniformly distributed random number(RN) among [1-RIGHT,2-LEFT,3-UP,4-DOWN]
b) If RN is 1, move right. Mark the new position
c) If RN is 2, move left. Mark the new position
d) If RN is 3, move up. Mark the new position
e) If RN is 4, move down. Mark the new position
f) Update all the traced positions to a 2D array - Visualize the 2D array which has recorded the trace of Random Walk.
Matlab Code (Random Walk)
% A code for simulating the random walk
clear,clc,close all
% clear - delete all variables from matlab memory
% clc - clear screen
% close all - close all matlab figure windows
space_2d=zeros(121,121);
x=61;
y=61;
space_2d(x,y)=1;
% We are going to play random walk here
for i=1:1000
direction=randi(4);
% randi(4) is a uniform distributed integer which spits out integers 1 to 4
% Let 1 imply right,2 - up, 3 - left, 4 - down
if direction==1
x=x+1;
space_2d(x,y)=1;
elseif direction==2
y=y+1;
space_2d(x,y)=1;
elseif direction==3
x=x-1;
space_2d(x,y)=1;
elseif direction==4
y=y-1;
space_2d(x,y)=1;
end
end
imagesc(space_2d) % Visualize the Random walker trace
Ensemble of Random Walks and Diffusion
Let us inspect few outputs from the above program:
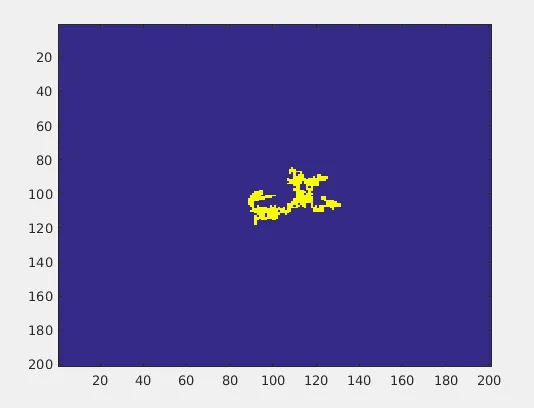
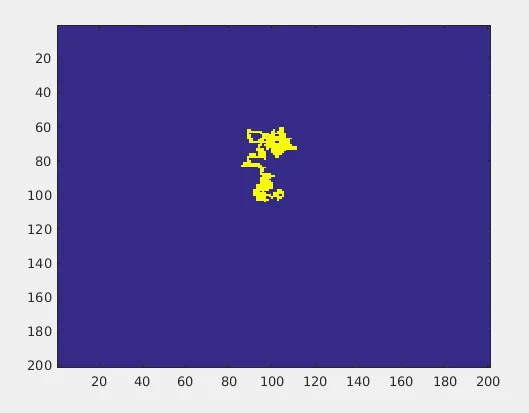
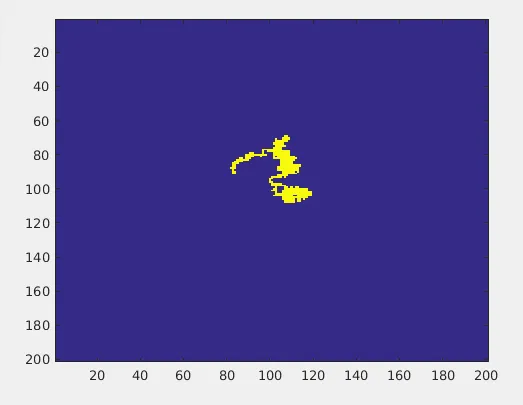
Each run gives you different trajectories. The Random walk program actually generates an ENSEMBLE of outcomes. What will be the averaged version of N Random Walks? As N tends to infinity(or large enough), the averaged version of these random walks tends to give an output as below:
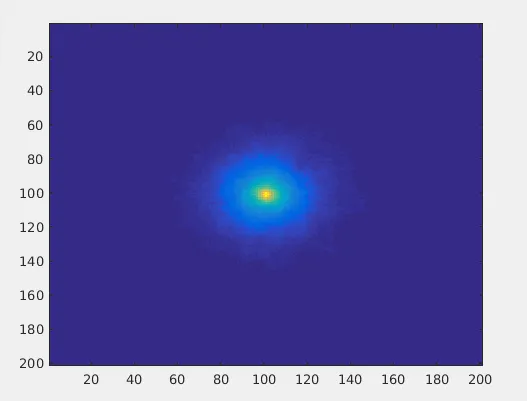
The above figure is an example of diffusion. More concentration at the center and as you move away from the center the concentration goes down. If we let the particle move forever, the diffusion diagram will look more flatter in concentration as if an ink drop is spread totally in a glass of water.
Matlab Code (Diffusion)
% A code for simulate diffusion from 1000 random walks
clear,clc,close all
% clear - delete all variables from matlab memory
% clc - clear screen
% close all - close all matlab figure windows
space_2d=zeros(201,201,100);
x=101;
y=101;
space_2d(x,y,1)=1;
% We are going to play random walk here
for repeat=1:1000
x=101;
y=101;
for i=1:1000
direction=randi(4);
% randi(4) is a uniform distributed integer which spits out integers 1 to 4
% Let 1 imply right,2 - up, 3 - left, 4 - down
if direction==1
x=x+1;
space_2d(x,y,repeat)=1;
elseif direction==2
y=y+1;
space_2d(x,y,repeat)=1;
elseif direction==3
x=x-1;
space_2d(x,y,repeat)=1;
elseif direction==4
y=y-1;
space_2d(x,y,repeat)=1;
end
end
end
imagesc(mean(space_2d,3)) %Visualize the averaged traces of all 1000 Random Walks
You can find all the codes used in this article at my Github page too. Link: https://github.com/dexterdev/STEEMIT/tree/master/DIFFUSION_from_Random_Walk
Bonus Section: An exercise
So here we saw how to simulate a Random Walk and Diffusion process in 2D using Matlab. In my opinion, the random walk code was minimal and dirty. In fact, you can illustrate it better through an animation by showing the evolution of path which is traced by the Random walker. You may try doing that if interested.
References (for further reading)
- Random Walks in Biology By Howard C. Berg
- Elements of Random Walk and Diffusion Processes By Oliver C. Ibe
Join #steemSTEM
#steemSTEM is a community project with the goal to promote and support Science, Technology, Engineering and Mathematics related content and activities on the STEEM blockchain. If you wish to support the #steemSTEM project you can: Contribute STEM content using the #steemstem tag | Support steemstem authors | Join our curation trail | Join our Discord community | Delegate SP to steemstem
Convenient Delegation Links:

Follow me @dexterdev
____ _______ ______ _________ ____ ______
/ _ / __\ \//__ __/ __/ __/ _ / __/ \ |\
| | \| \ \ / / \ | \ | \/| | \| \ | | //
| |_/| /_ / \ | | | /_| | |_/| /_| \//
\____\____/__/\\ \_/ \____\_/\_\____\____\__/